質量分析屋の髙橋です。ペプチドやタンパク質など、分子内にアミノ基などプロトン受容性の官能基を複数もつ物質を正イオン検出のエレクトロスプレーで測定すると、1つの分子に対して複数のプロトンが付加した多価イオンが生成し易い事は良く知られています。
マススペクトルの横軸はm/z(mはイオンの質量を統一原子質量単位で割った値、zはイオンの電荷数)で表され、zが1の時つまりは1価イオンでは、m/zはイオンの質量と等しくなり、イオンのm/z値とイオン種から元の分子の質量を推測する事が出来ます。
一方、zが複数の時つまり多価イオンの場合、m/zとイオンの質量は大きく異なり、イオンの電荷数が分からないと元の分子の質量や分子量を推測する事は出来ません。
多価イオンのマススペクトル解析では、イオンの電荷数を知る事は極めて重要です。
ここでは、ペプチドやタンパク質の正イオンエレクトロスプレーにより得られたマススペクトルを例にとり、多価イオンの電荷数を判断する方法を2つ解説します。
1.同位体の分離挙動から判断する方法
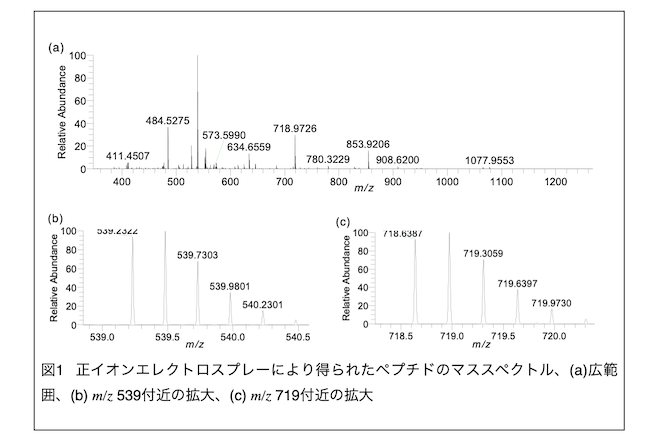
これは、同位体ピークのm/z差から電荷数を判断する方法です。以前のこの記事で、マススペクトルにおいて観測される同位体ピークについて解説しています。C, H, N, Oを中心に構成される通常の有機化合物のマススペクトルでは、モノアイソトピックピークに対して約+1の質量をもつ同位体ピークの大部分は、13Cを1つ含む分子由来です。同位体の質量差は約1なので、1価イオンの場合、同位体ピークのm/z差は1になります。ところが多価イオンでは、マススペクトルの横軸はm/zなので、同位体ピークのm/z差は1を電荷数で割った値、即ち2価イオンでは約0.5、3価イオンでは約0.33になります。実際のマススペクトルで確認してみましょう。図1に正イオンエレクトロスプレーにより得られたペプチドのマススペクトルを示します。(a)は測定した全m/z範囲での表示、(b)はm/z 539付近の拡大表示、(c)はm/z 719付近の拡大表示です。(b)と(c)のスペクトルはそれぞれ同位体ピークが分離されている様子を示しています。その同位体ピークのm/z差に着目すると、(b)では約0.25、(c)では約0.33であり、(b)は4価イオン([M+4H]4+)、(c)は3価イオン([M+3H]3+)である事が分かります。尚、このスペクトルはギ酸を添加した水/アセトニトリルのグラジエント溶離条件で得られたもので、この条件において、ペプチドは先ず間違いなくプロトン付加分子として検出されます。そして、このペプチドの実測値としてのモノアイソトピック質量を計算する場合は、(b), (c)の各モノアイソトピックピークのm/z値とイオン種の情報から、以下の様になります。
・4価イオン:539.2322×4-(1.0073×4)=2 152.8996
・3価イオン:718.6387×3-(1.0073×3)=2 152.8942
平均:2,152.8969
このように、同位体ピークの分離挙動から多価イオンの電荷数を明確に判断できるのは、ペプチドの質量(分子量)に対して装置の質量分解能が十分に高いためです。
2.一次方程式を使う方法
では、分子サイズ(分子の質量、分子量)に対して、同位体を分離出来ない条件即ち質量分解能の低い装置を使った場合はどうなるでしょうか?
図2 正イオンエレクトロスプレー+低分解能の質量分析計で得られたタンパク質のマススペクトル 図1で示したような多価イオンの同位体ピークが分離出来ないため、1つ1つの多価イオンから電荷数を判断する事は出来ません。その場合、同一の物質(ペプチドやタンパク質)から生成した複数の多価イオンを使って、一次方程式から多価イオンの電荷数を計算する事ができます。
図2に、或るタンパク質を正イオンエレクトロスプレー+低分解能の質量分析計で得られたマススペクトルを示します。電荷数の分布を示す、典型的なタンパク質の多価イオンのマススペクトルです。低分解能の装置で得られているため、各多価イオンを横軸方向に拡大しても、図1(b), (c)で示したような同位体ピークの分離は確認できません。
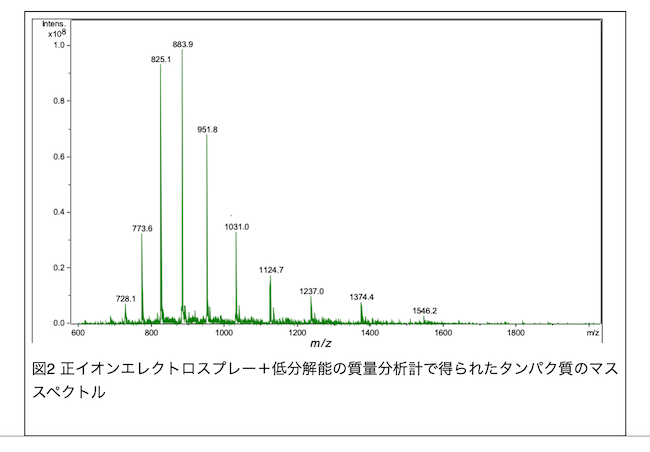
この様な場合、2つの異なる電荷数の多価イオンのm/z値を用いて、電荷数を計算できます。例えばメインピークであるm/z 883.9イオンをx価とすると、2番目に大きなm/z 825.1イオンは(x+1)価となります。全てプロトン付加イオンであると仮定すると、次の式が成り立ちます。低分解能装置を用いているため、プロトンの質量は1とします。
883.9x-x=825.1(x+1)-(x+1)
883.9x-825.1x=825.1-1
58.8x=824.1
x=14.015
電荷数は必ず整数なので、m/z 883.9イオンは14価である事が分かりました。2番目に大きなm/z 825.1イオンは15価、m/z 951.8イオンは13価なので、これら3つのイオンを使って元のタンパク質の分子量を計算すると、
825.1×15-15=12,361.5
883.9×14-14=12,360.6
951.8×13-13=12,360.4
平均:12,360.8
となります。デコンボリューションのソフトを使うとこの計算をしてくれますが、手計算でも結構簡単でしょ! 覚えておいて損はないと思います。因みに、このタンパク質の例では、同位体ピークが分離されていないので、得られるのは分子の質量ではなく分子量となります。




